অষ্টম (৮ম) শ্রেণি গণিত ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট প্রশ্ন ও সমাধান
শিরোনামঃ ৩নং গণিত অ্যাসাইনমেন্ট
আরো পড়ুনঃ
- ৮ম শ্রেণির বাংলাদেশ ও বিশ্বপরিচয় অ্যাসাইনমেন্ট ২য় সপ্তাহ ২০২১ উত্তর।
- ১ম সপ্তাহের সকল গ্রিড ও এ্যাসাইনমেন্ট প্রশ্ন ও সমাধান ২০২১ (৬ষ্ঠ থেকে ৯ম শ্রেণি)
- (৮ম) অষ্টম শ্রেণির বাংলা এসাইনমেন্ট ১ম সপ্তাহ ২০২১ প্রশ্ন ও সমাধান
- অষ্টম শ্রেণির ইসলাম এসাইনমেন্ট ১ম সপ্তাহ ২০২১ সমাধান
আরো দেখুন:
- ৮ম শ্রেণি বাংলা ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
- ৮ম শ্রেণি কৃষি ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
- ৮ম শ্রেণি গার্হস্থ্য ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
৮ম গণিত ষষ্ঠ সপ্তাহের প্রশ্নগুলো দেখুনঃ
সৃজনশীল প্রশ্ন:১. রফিকের পিতা এবং রফিকের 5 বছর পূর্বে বয়সের অনুপাত ছিল 10:4 এবং 5 বছর পরে রফিকের পিতা ও রফিকের বয়সের অনুপাত হবে 2:1।ক. প্রদত্ত তথ্যের আলোকে দুইটি সমীকরণ গঠন কর।খ. প্রতিস্থাপন পদ্ধতি ব্যবহার করে, তাদের দুইজনের বর্তমান বয়স নির্ণয় কর।গ. “ক’ হতে প্রাপ্ত সমীকরণদ্বয় লেখের সাহায্যে সমাধান করে, “খ” এর উত্তরের সত্যতা যাচাই কর।সংক্ষিন্ত প্রশ্ন: ক১. পিথাগোরাসের উপপাদ্যটি বিবৃত কর?২. একটি সমকোণী ত্রিভুজের একটি বাহু ও অতিভুজের অনুপাত 5:13 হলে, অপর বাহু কত?৩. কোন ত্রিভুজের তিনটি বাহর দৈর্ঘ্যের এমনভাবে অনুপাত লিখ, যা দ্বারা একটি সমকোনী ত্রিভুজ আকাসম্ভব?8. ABC ত্রিভুজের AB²=BC²+CA² হলে, কোন কোণটি সমকোণ হবে?সংক্ষিন্ত প্রশ্ন: খ১. আয়ত এবং আয়তক্ষেত্রের মধ্যে পার্থক্য কোথায়?২. ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়ের সূত্রটি লিখ।৩. ঘনক আর ঘনবন্তুর মধ্যে পার্থক্য কোথায়?8. একটি সমবৃত্তডুমিক বেলনের ব্যাসার্ধ 3.75 সে.মি. ও উচ্চতা 11.50 সে.মি। বেলনটির সমগ্রতলের ক্ষেত্রফল কত?৫. একটি চতুর্ভুজ আকতে কমপক্ষে কয়টি অনন্য নিরপেক্ষ উপাত্তের প্রয়োজন?৬. যে কোন সরলরেখা একটি বৃন্তকে সর্বাধিক কয়টি বিন্দুতে ছেদ করতে পারে?৭. একটি চাকার ব্যাসার্ধ 34 সে.মি. হলে, চাকাটি একবার ঘুরলে কত সে.মি. দূরত্ব অতিক্রম করবে?সৃজনশীল প্রশ্ন: ০৩১. কোনো বর্গের পরিসীমা 12 সে.মি. এবং একটি আয়তের বাহুর দৈর্ঘ্য 2 সে.মি. ।ক. চিত্রসহ ঘুড়ির সংগা লিখ।খ. অঙ্কনের বিবরণসহ উদ্দীপকের আলোকে বর্গটি আক।গ. ‘খ’ তে অঞ্রিত বর্গের কর্ণকে উদ্দীপকের আয়তের কর্ণ ধরে, আয়তটি জাক। (অঞ্জনের বিবরণসহ)
সৃজনশীল প্রশ্ন-১
১ এর ’ক’ প্রশ্নের উত্তর
মনেকরি,
পিতার বর্তমান বয়স x বছর।
পূত্রের বর্তমান বয়স y বছর।
5 বছর পূর্বে পিতার বয়স x-5 বছর।
5 বছর পূর্বে পূত্রের বয়স y-5 বছর।
এবং 5 বছর পর পিতার বয়স x+5 বছর।
5 বছর পর পূত্রের বয়স y+5 বছর।
প্রশ্নমতে, (x-5):(y-5) = 10:4
বা, (x-5)/(y-5) = 10/4
বা, (x-5)/(y-5) = 5/2
বা, 2x-10 = 5y-25
বা, 2x-5y -10+25 = 0
∴ 2x-5y+15=0
আবার, (x+5):(y+5) = 2:1
বা, (x+5)/(y+5) = 2/1
বা, x+5 = 2y+10
বা, x-2y+5-10 = 0
∴ x-2y-5 = 0
১ এর ’খ’ প্রশ্নের উত্তর
’ক’ হতে পাই, 2x-5y+15=0 ——-(i)
এবং x-2y-5 = 0
বা, x = 2y+5 ——-(ii)
x এর মান সমীকরণ (i) এ বসিয়ে পাই
2(2y+5) -5y+15=0
বা, 4y+10-5y+15 = 0
বা, -y+25=0
বা, -y=-25
∴ y=25
y এর মান সমীকরণ (ii) এ বসিয়ে পাই
x = 2×25+5
= 50+5
= 55
∴ পিতার বর্তমান বয়স 55 বছর।
পূত্রের বর্তমান বয়স 25 বছর।
১ এর ’গ’ প্রশ্নের উত্তর
’ক’ হতে পাই,
2x-5y+15=0
2x=5y-15
∴ x = (5y-15)/2 ——-(iii)
এবং x-2y-5 = 0
∴ x = 2y+5 ——(iv)
সমীকরণ (iii) ও (iv) হতে y এর ভিন্ন ভিন্ন মানের জন্য x এর প্রাসঙ্গিক মান নির্ণয় করি।
|
y |
5 |
25 |
35 |
|
x |
5 |
55 |
80 |
|
y |
5 |
-5 |
25 |
|
x |
15 |
-5 |
55 |
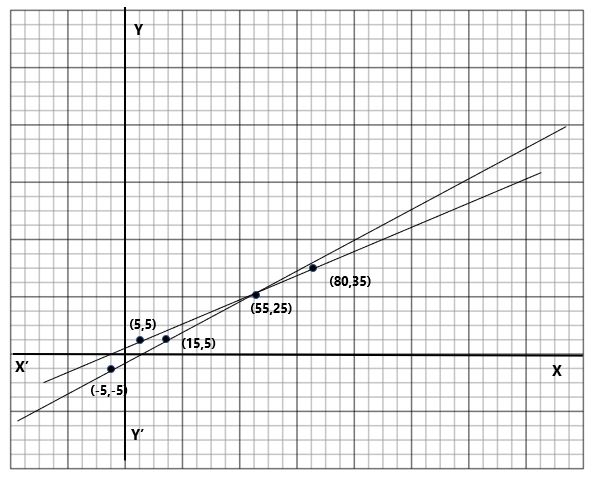
ছক কাগজের X অক্ষ বরাবর 1 ঘর সমান x এর 5 একক এবং Y অক্ষ বরাবর 1 ঘর সমান y এর 5 একক নিয়ে লেখচিত্র অঙ্কন করি।
উপরের প্রথম ছকের (5,5) (55,25), ও (80,35) বিন্দুগুলো ছক কাগজে স্থাপন করি এবং একটি সরলরেখা পাওয়া গেল।
আবার, দ্বিতীয় ছকের (15,5), (-5,-5) ও (55,25) বিন্দুগুলো ছক কাগজে স্থাপন করি এবং অপর একটি সরলরেখা পাওয়া গেল।
সংক্ষিপ্ত প্রশ্নের উত্তর
ABC ত্রিভূজে AB²=BC²+CA²
পীথাগোরাসের উপপাদ্য অনুসারে,
অতিভূজ ² = লম্ব ² + ভূমি ²
তুলনা করে পাই, অতিভূজ= AB
লম্ব= BC
ভূমি = CA
∴ অতিভূজ AB এর বিপরীত কোন সমকোন অর্থাৎ ∠ABC কোনটি সমকোণ।
সংক্ষিপ্ত প্রশ্ন ’খ’এর(১) উত্তর
যে সামান্তরিকের একটি কোন সমকোন তাকে আয়ত বলে। আয়তের চারটি কোনই সমকোণ।
অপরদিকে আয়ত দ্বারা আবদ্ধ ক্ষেত্র কে আয়তক্ষেত্র বলে।
সংক্ষিপ্ত প্রশ্ন ’খ’এর(২) উত্তর
ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়ের সূত্রটি হলো।
ট্রাপিজিয়ামের ক্ষেত্রফল = সমান্তরাল বাহুদ্বয়ের সমষ্টির গড়×উচ্চতা।
সংক্ষিপ্ত প্রশ্ন ’খ’এর(৩) উত্তর
যে সকল বস্তুর দৈর্ঘ্য , প্রস্থ ও উচ্চতা আছে, তাদেরকে ঘনবস্তু বলে। ঘনবস্তু আয়তাকার, বর্গাকার, বা গোলাকারও হতে পারে।
অপরদিকে, যে সকল বর্গাকার ঘনবস্তুর মোট ছয়টি পরস্পর সমান বর্গাকার পৃষ্ঠ বা তল আছে যাদের প্রত্যেকটি একটি বর্গক্ষেত্র এবং পরস্পর বিপরীত পৃষ্ঠদ্বয় সমান্তরাল, তাকে বর্গাকার ঘনবস্তু বা ঘনক বলে।
সংক্ষিপ্ত প্রশ্ন ’খ’এর(৪) উত্তর
দেওয়া আছে, বেলনের ব্যাসার্ধ, r = 3.75cm
বেলনের উচ্চতা , h=11.50cm
∴ বেলনটির সমগ্রতলের ক্ষেত্রফল = 2πr(r+h)
= 2×3.1416×3.75(3.75+11.50)
= 2×3.1416×3.75×15.25
= 359.32cm²
সংক্ষিপ্ত প্রশ্ন ’খ’এর(৫) উত্তর
একট চতুর্ভূজ আঁকতে কমপক্ষে পাঁচটি অনন্য উপাত্তের প্রয়োজন।
সংক্ষিপ্ত প্রশ্ন ’খ’এর(৬) উত্তর
যে কোনো সরলরেখা একটি বৃত্তকে সর্বাধিক দুইটি বিন্দুতে ছেদ করতে পারে।
সংক্ষিপ্ত প্রশ্ন ’খ’এর(৭) উত্তর
দেওয়া আছে,
চাকার ব্যাসার্ধ, r = 34cm
∴ চাকার পরিধি = 2πr
= 2×3.1416×34
= 213.6288 cm
যেহেতু চাকাটি একবার ঘুরলে তার পরিধি সমান দুরুত্ব অতিক্রম করে।
∴ চাকাটি একবার ঘুরলে 213.6288 cm দুরুত্ব অতিক্রম করবে।
সৃজনশীল প্রশ্ন ৩
৩ এর ‘ক’প্রশ্নের উত্তর
ঘুড়ি: যে চতুর্ভূজের দুই জোড়া সন্নিহিত বাহু সমান তাকে ঘুড়ি বলে।
৩ এর ‘খ’প্রশ্নের উত্তর
দেওয়া আছে,
বর্গের পরিসীমা p=12cm
বর্গটি আঁকতে হবে।
অঙ্কনঃ পরিসীমাকে সমান চারভাগে বিভক্ত করি। যেকোনো রশ্মি AE হতে p/4
এর সমান ব্যাসার্ধ্য নিয়ে AB অংশ কেটে নিই। A বিন্দুতে AB এর উপর AF লম্ব আঁকি। AF হতে p/4 এর সমান করে AD অংশ কেটে নিই। এখন B ও D কে কেন্দ্র করে p/4 এর সমান ব্যাসার্ধ নিয়ে ∠BAD এর অভ্যন্তরে দুইটি বৃত্তচাপ অঙ্কন করি। মনে করি বৃত্তচাপ দুটি পরস্পর C বিন্দুতে ছেদ করে। BC ও CD যোগ করি।
তাহলে ∆ABC ই নির্ণেয় ত্রিভূজ।
৩ এর ‘গ’প্রশ্নের উত্তর
ধরি ’খ’ তে অঙ্কিত বর্গের কর্ণ যা আয়তের কর্ণ
অঙ্কনঃ যেকোনো রশ্মি AE হতে b এর সমন করে AB অংশ কেটে নিই। A বিন্দুতে AB এর উপর AF লম্ব আঁকি।
B বিন্দু থেকে a এর সমান ব্যাসর্ধ্য নিয়ে একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি AF কে D বিন্দুতে ছেদ করে। এখন A ও D বিন্দুকে কেন্দ্র করে যথাক্রমে a ও b এর সমান ব্যসার্ধ নিয়ে ∠BAD এর অভ্যন্তরে দুইটি বৃত্তচাপ অঙ্কন করি। মনে করি বৃত্তচাপ দুটি পরস্পর C বিন্দুতে ছেদ করে।
তাহলে ABCD ই নির্ণেয় আয়ত।
আরো দেখুন:
- ৮ম শ্রেণি বাংলা ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
- ৮ম শ্রেণি কৃষি ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
- ৮ম শ্রেণি গার্হস্থ্য ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
সকল অ্যাসাইনমেন্টের জন্য নিচের ফেজবুক পেজটিতে লাইক দিয়ে রাখুন।