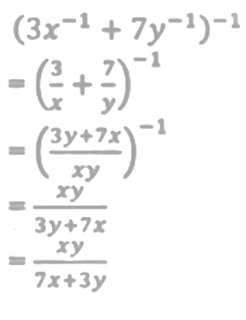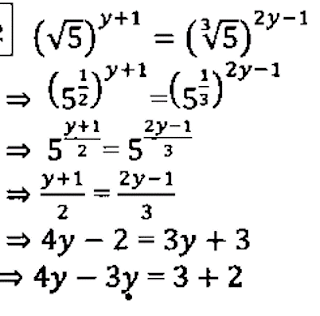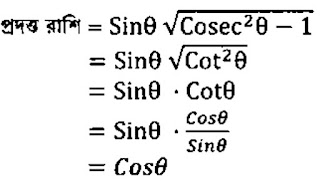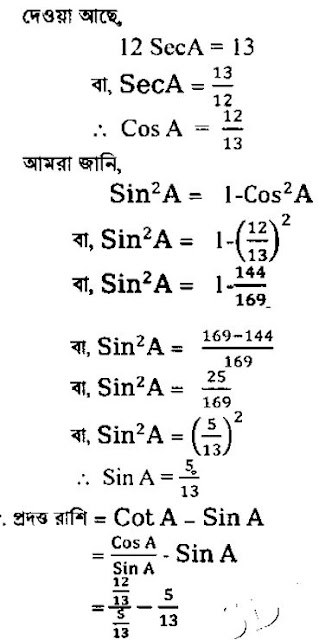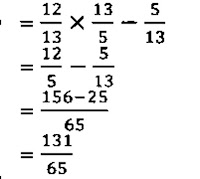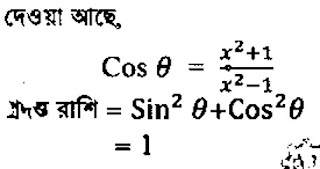নবম (৯ম) শ্রেণি গণিত ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট class 9 math 6th week’s assignment

শিরোনামঃ ৩নং গণিত অ্যাসাইনমেন্ট

আরো পড়ুনঃ

১ম সপ্তাহের সকল গ্রিড ও এ্যাসাইনমেন্ট প্রশ্ন ও সমাধান ২০২১ (৬ষ্ঠ থেকে ৯ম শ্রেণি)

আরো দেখুনঃ

৩য় সপ্তাহের (৯ম) নবম শ্রেণির কৃষি শিক্ষা এসাইনমেন্ট উত্তর ২০২১।
৩য় সপ্তাহ (৯ম) নবম শ্রেণির উচ্চতর গণিত অ্যাসাইনমেন্ট সমাধান ২০২১
৯ম শ্রেণি পদার্থ ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট
৯ম শ্রেণি বিজ্ঞান ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট
৯ম শ্রেণি বা ও বি ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট
৯ম শ্রেণি হিসাববিজ্ঞান ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট

নবম শ্রেণির ৬ষ্ঠ সপ্তাহের গণিত প্রশ্নগুলো দেখতে এখানে ক্লিক করুন।

অ্যাসাইনমেন্ট শুরু

সংক্ষিপ্ত প্রশ্ন ০১ এর উত্তর

সংক্ষিপ্ত ০১ এর ১ প্রশ্নের উত্তর।

নির্দিষ্ট চতুর্ভূজ আঁকার জন্য পাঁচটি স্বতন্ত্র উপাত্তের প্রয়োজন। যথা:

চারটি বাহ ও একটি কোণ
চারটি বাহ ও একটি কর্ণ
তিনটি বাহু ও দুইটি কর্ণ
তিনটি বাহ ও এদের অন্তর্ভুক্ত কোণ
দুইটি বাহু ও তিনটি কোণ

সংক্ষিপ্ত ০১ এর ২ প্রশ্নের উত্তর।

মনে করি O কেন্দ্রবিশিষ্ট ABC বৃত্তে ∠BOC কেন্দ্রস্থ সরণ কোন এবং ∠BAC বৃত্তস্থ কোণ।

আমরা জানি, একই চাপের উপর দণ্ডায়মান বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক।

∴ বৃত্তস্থ কোণ, ∠BAC = কেন্দ্রস্থ ∠BOC ÷ ২

= 180⁰ ÷ ২

= 90⁰

সংক্ষিপ্ত ০১ এর ৩ প্রশ্নের উত্তর।

সমকোণী ত্রিভূজের সুক্ষকোণদ্বয় সমান হলে ত্রিভূজটির বাহুগুলোর অনুপাত হবে।

1:1:√2

সংক্ষিপ্ত ০১ এর ৪ প্রশ্নের উত্তর।

দেওয়া আছে, ∠P = ∠R এবং ∠Q = ∠S = 84==95⁰

আমরা জানি, সামান্তরিকের চারটি কোণের সমষ্টি 360⁰

অর্থাৎ ∠P + ∠R +∠Q + ∠S = 360⁰

বা, ∠R + ∠R +95⁰ + 95⁰ = 360⁰

বা, 2∠R = 360⁰-190⁰

বা, ∠R= 170⁰÷ ২

∴ ∠R = 85⁰

∴ ∠S- ∠R= 95⁰- 85⁰ = 10⁰

সংক্ষিপ্ত ০১ এর ৫ প্রশ্নের উত্তর।

মনেকরি, বৃত্তের ব্যাস, AC = 14cm

এবং বর্গের এক বাহুর দৈর্ঘ্য = a cm

∴ বর্গের কর্ণের দৈর্ঘ্য = বৃত্তের ব্যাস

বা, √2a = 14

বা, a = 14 ÷ √2

বা, a = 7√2

বা, a² = (7√2)²

বা, a² = 98

∴ বর্গের ক্ষেত্রফল a² = 98 cm²

সৃজনশীল প্রশ্ন ০১ এর উত্তর

সৃজনশীল প্রশ্ন ১ এর ‘ক’উত্তর

দেওয়া আছে, ∆ABC এ ∠B = 45⁰, ∠C = 60⁰

আমরা জানি, ত্রিভুজের তিন কোণের সমষ্টি = 180⁰

সুতরাং ∠A+∠B+∠C = 180⁰

বা, ∠A+45⁰,+60⁰ = 180⁰

বা, ∠A = 180⁰- 105⁰

∴ ∠A = 75⁰

সুতরাং ∠A কোণের পূরক কোণ = 90⁰-75⁰= 15⁰

সৃজনশীল প্রশ্ন ১ এর ‘খ’ উত্তর

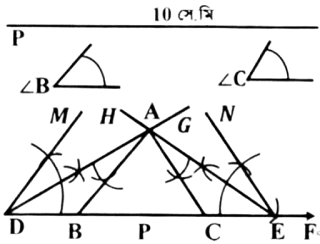
বিশেষ নির্বচনঃ দেওয়া আছে, ABC ত্রিভূজের ভূমি সংলগ্ন দুইটি কোণ ∠B =45⁰ ও ∠C = 60⁰ এবং পরিসীমা P =10 সে.মি। ত্রিভূজটি আঁকতে হবে।

নবম (৯ম) শ্রেণি গণিত ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট ৩

অঙ্কনঃ যেকোন রশ্মি DF থেকে DE=P কেটে নিই। DE রেখাংশের একই পাশে D ও E বিন্দুতে ∠EDM = ∠B এবং ∠DEN=∠C আঁকি।কোণ দুইটির সমদ্বিখন্ডক DG ও EH পরস্পর A বিন্দুতে ছেদ করে। A বিন্দুতে ∠ADE = ∠DAB এবং ∠AED = ∠EAC আঁকি। AB ও AC রশ্মিদ্বয় DE রেখাংশের B ও C বিন্দুতে ছেদ করে।

তাহলে ∆ABC ই উদ্দিষ্ট ত্রিভূজ।

সৃজনশীল প্রশ্ন ১ এর ‘গ’ উত্তর

বিশেষ নির্বচনঃ দেওয়া আছে, ত্রিভূজের ভূমি সংলগ্ন দুটি কোন ∠B =45⁰ ও ∠C = 60⁰ এবং শীর্ষ থেকে ভূমির উপর অঙ্কিত লশ্বের দৈর্ঘ্য 10÷3 = 3.33cm। ত্রিভূজটি আঁকতে হবে।।

অঙ্কনঃ যেকোন সরলরেখা AG থেকে d এর সমান করে AD অংশ কেটি নিই। AD রেখার A ও D বিন্দুতে যথাক্রমে PAQ এবং MDN লম্ব আঁকি। PQ রেখার ‍A বিন্দুতে ∠PAB = ∠B এবং ∠QAC = ∠C আঁকি। AB ও AC রেখা দুইট MN কে B ও C বিন্দুতে ছেদ করে।

তাহলে, ∆ABC ই উদ্দিষ্ট ত্রিভূজ।