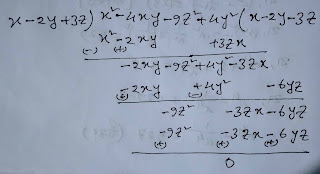সপ্তম (৭ম) শ্রেণির গণিত ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্টের প্রশ্ন ও সমাধান (নির্ভূল সমাধান)

শিরোনামঃ ৩নং গণিত অ্যাসাইনমেন্ট

আরো দেখুনঃ

• ৭ম বাংলা ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
• ৭ম কৃষি ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
• ৭ম গার্হস্থ্য ৬ষ্ঠ সপ্তাহের অ্যাসাইনমেন্ট সমাধান
• ৬ষ্ঠ সপ্তাহের সকল শ্রেণির অ্যাসাইনমেন্ট সমাধান

৭ম শ্রেণি গণিত ৬ষ্ঠ সপ্তাহের প্রশ্নগুলো দেখুন।

প্রশ্ন: ০১

তোমার গণিত বইয়ের দৈর্ঘ্যের এক চতুর্থাংশ, প্রস্থের এক তৃতীয়াংশ এবং তোমার কলমের দৈর্ঘের অর্ধাংশ পরিমাপ করে, প্রাপ্ত তথ্যগুলো ব্যবহার করে নিচের প্রশ্নগুলোর উত্তর দাও।

(ক) পরিমাপকৃত বাহগুলোর দ্বারা ত্রিভুজ অংকন কর।

(খ) দেখাও যে, অংকনকৃত ত্রিভুজের কোণগুলোর মধ্যে বৃহত্তম বাহুর বিপরীত কোণটি বৃহত্তম।

(গ) ত্রিভুজটির কোণ তিনটিকে কেটে জালাদা করে এক বিন্দুতে স্থাপন করে দেখাও যে. তিনটি কোণ একত্রে এক সরলকোণ তৈরি করে।

প্রশ্ন: ০২

তোমার ৩০ জন সহপাঠীর উচ্চতা (আসন্ন সেন্টিমিটারের মানে) সংগ্রহ কর এবং তা তোমার খাতায় লিপিবদ্ধ কর।

(ক) উপাত্তগুলোকে মানের ক্রমানুসারে সাজাও।

(খ) সর্বোচ্চ সংখ্যক সহপাঠী কত উচ্চতা বিশিষ্ট তা আয়তলেখের সাহায্যে নির্ণয় কর।

সৃজনশীল প্রশ্নের উত্তর

১এর ‘ক’ প্রশ্নের উত্তর

আমার গণিত বইয়ের দৈর্ঘ্য =  24cm

∴ বইয়ের দৈর্ঘ্যের চতুর্থাংশ =  24 এর 1/ 4 = 6cm

আমার গণিত বইয়ের প্রস্থ = 18cm

∴ বইয়ের প্রস্থের এক তৃতীয়াংশ = 18 এর 1/3 = 6 cm

আমার কলমের দৈর্ঘ্য = 14cm

∴ কলমের দৈর্ঘ্যের অর্ধ্যাংশ = 14/2= 7 cm

সুতরাং ত্রিভূজের তিন বাহুর দৈর্ঘ্য যথাক্রমে

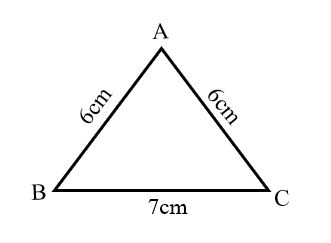
    a=6cm, b=6cm, c= 7cm

পরিমাপকৃত বাহুগুলো দ্বারা ত্রিভূজ অঙ্কন করা হলো:

১এর ‘খ’ প্রশ্নের উত্তর

’ক’ তে অঙ্কিত ত্রিভূজ থেকে আমরা জানি,

ত্রিভুজের ABC এর বৃহত্তম বাহু BC(7cm) এর বিপরীত কোন ∠BAC 

প্রমাণ করতে হবে যে ∠BAC  ত্রিভূজের বৃহত্তম কোন।

প্রমাণঃ 

    ধাপ-১ঃ যেহেতু BC﹥AB

        ∴ ∠BAC﹥∠ACB [ত্রিভূজের বৃহত্তর বাহুর বিপরীত কোন, ক্ষুদ্রতর বাহুর বিপরীত কোন অপেক্ষা বৃহত্তর]

    ধাপ-১ঃ যেহেতু BC﹥AC

        ∴ ∠BAC﹥∠ABC

        ∴ ∠BAC ত্রিভূজটির বৃহত্তম কোণ।

১এর ‘গ’ প্রশ্নের উত্তর

’ক’ হতে প্রাপ্ত ত্রিভূজটির কোনগুলোকে কেটে আলাদা করে একটি ‍বিন্দুতে পাশের চিত্রের মতো করে স্থাপন করা হলো

২এর ‘ক’ প্রশ্নের উত্তর

সংগৃহীত উপাত্তঃ ১৫০, ১৪৬, ১৪৮, ১৪৯, ১৪৫, ১৪৫, ১৪৫, ১৪৬, ১৪৭, ১৪৭, ১৪৭, ১৪৭, ১৪৭, ১৪৭, ১৪৭, ১৪৭, ১৪৮, ১৪৮, ১৪৮, ১৪৮, ১৪৮, ১৪৮, ১৪৯, ১৪৯, ১৪৯, ১৪৯, ১৫০, ১৫০, ১৫০, ১৫০

উপাত্তগুলোকে মানের উধ্বক্রমে সাজিয়ে পাই- ১৪৫, ১৪৫, ১৪৫, ১৪৬, ১৪৬, ১৪৭, ১৪৭,১৪৭,১৪৭,১৪৭,১৪৭,১৪৭, ১৪৮, ১৪৮, ১৪৮, ১৪৮, ১৪৮, ১৪৮, ১৪৮, ১৪৯, ১৪৯, ১৪৯, ১৪৯, ১৪৯, ১৫০, ১৫০, ১৫০, ১৫০, ১৫০

২এর ‘খ’ প্রশ্নের উত্তর

উপাত্তগুলোকে সারণিবদ্ধ করে পাই:

উচ্চতা	১৪৫	১৪৬	১৪৭	১৪৮	১৪৯	১৫০
গণসংখ্যা	৩	২	৮	৭	৫	৫

X  অক্ষ বরাবর উচ্চতা এবং Y অক্ষ বরাবর গণসংখ্যা নিয়ে আয়তলেখ অঙ্কন করি যেখানে

X অক্ষের ৫ঘর সমান উচ্চতার ১ একক এবং Y অক্ষের ২ ঘর সমান গনসংখ্যার ১ একক ধরে আয়তলেখ অঙ্কন করি। X অক্ষে ০ থেকে ১৪৫ পর্যন্ত ভাঙা রেখা দ্বারা দেখানো হয়েছে।

সংক্ষিপ্ত প্রশ্নের উত্তর

∴ অপর উৎপাদক = (x-2y-3z)

৮ এর i) বামপক্ষ = (2x+3y)(2x-3y)
        = (2x)²-(3y)²
        = 4x²-9y²
        = ডানপক্ষ
    ∴বামপক্ষ=ডানপক্ষ

৮ এর ii) বামপক্ষ = 1/2 {(m-n)²+(m+n)²}
        = 1/2×2(m²+n²)
        = (m²+n²)
        = ডানপক্ষ
∴বামপক্ষ=ডানপক্ষ

৮ এর iii) বামপক্ষ = (a+b)²+4ab
        ≠ (a-b)²
        ≠ ডানপক্ষ
    ∴বামপক্ষ ≠ ডানপক্ষ

৯) দেওয়া আছে, (x-y)² = 29
        প্রদত্ত রাশি,  (x+y)²
        = (x-y)²+4xy
        = (29)²+4xy

১০) প্রদত্ত রাশি, = x²+5x-6
        = x²-x+6x-6
        = x(x-1)+6(x-1)
        = (x-1)(x+6)

১১) প্রদত্ত সমীকরণ: 5(x-3)=10
      বা,   x-3 = 10/5
      বা,    x-3 = 2
      বা,    x=2+3

        ∴ x=5

প্রদত্ত সমীকরণের মূল হবে ৫

১২) প্রতিসাম্য বিধি অনুযায়ী, 2x+3=7x-5 কে 7x-5=2x+3 লেখা যায়।

১৩)  (-1,3) বিন্দুটি ২য় চতুর্ভাগে অবস্থিত

১৪) কোনো বিন্দুর ভূজের মান ০  হলে তা  x অক্ষরেখায়

১৫) মনে করি সংখ্যাটি = x

    প্রশ্নমতে, x-(-6) = -12

        বা, x+6=-12
        বা, x = -12-6
        বা, x = -18

        ∴ সংখ্যাটি = -18

১৬) মনে করি, সংখ্যাটি = x

        ∴ সংখ্যাটির এক চতুর্থাংশ = x এর 1/4 = x/4

        ∴ সংখ্যাটির এক তৃতীয়াংশ = x এর 1/3 = x/3

    প্রশ্নমতে, x/4 = x/3 – x/12